Show Mobile Notice

5 Applications Of The Derivative Part 2ap Calculus Using

1. Unit 5 - Applications of Integrals. Unit 6 - Rotations. Class Notes Part 2; Selection File type icon File name. Derivatives Guided Notes.docx.
2. Consider the curve given by + =𝟕+ (a) Show that =3 −2 8 −3 (b) Show that there is a point 𝑃 with an x-coordinate of 3 at which the line tangent to the curve at 𝑃 is.
3. Kranish AP Calculus. Home Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6. Unit 5 - Applications of the Derivative (Part 2).Quiz (Days 1 - 3): Wednesday, November 8th.

AP Calculus Applications of Derivatives. Showing 20 items from page AP Calculus Applications of Derivatives Part 1 Homework sorted by Assignment Number.

Chapter 4 : Applications of Derivatives

In the previous chapter we focused almost exclusively on the computation of derivatives. In this chapter will focus on applications of derivatives. It is important to always remember that we didn’t spend a whole chapter talking about computing derivatives just to be talking about them. There are many very important applications to derivatives.

The two main applications that we’ll be looking at in this chapter are using derivatives to determine information about graphs of functions and optimization problems. These will not be the only applications however. We will be revisiting limits and taking a look at an application of derivatives that will allow us to compute limits that we haven’t been able to compute previously. We will also see how derivatives can be used to estimate solutions to equations.

5 Applications Of The Derivative Part 2ap Calculus Class

Here is a listing of the topics in this section.

Rates of Change – In this section we review the main application/interpretation of derivatives from the previous chapter (i.e. rates of change) that we will be using in many of the applications in this chapter.

Critical Points – In this section we give the definition of critical points. Critical points will show up in most of the sections in this chapter, so it will be important to understand them and how to find them. We will work a number of examples illustrating how to find them for a wide variety of functions.

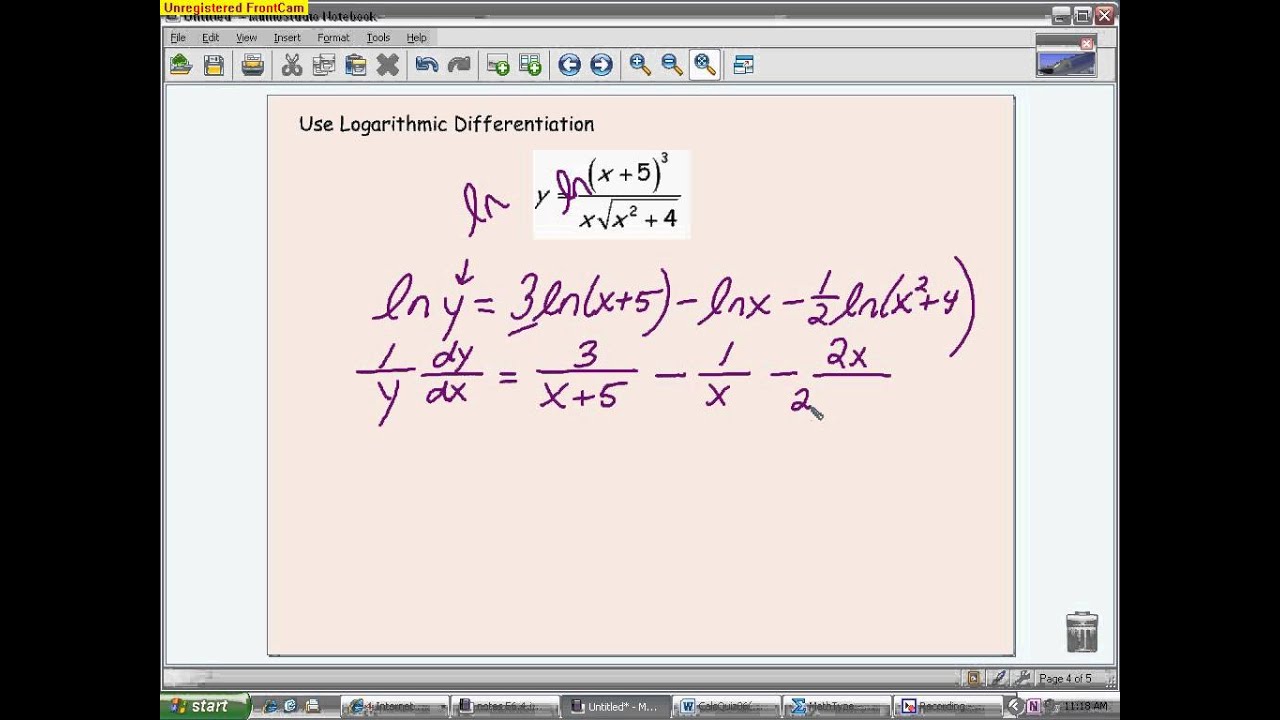
Minimum and Maximum Values – In this section we define absolute (or global) minimum and maximum values of a function and relative (or local) minimum and maximum values of a function. It is important to understand the difference between the two types of minimum/maximum (collectively called extrema) values for many of the applications in this chapter and so we use a variety of examples to help with this. We also give the Extreme Value Theorem and Fermat's Theorem, both of which are very important in the many of the applications we'll see in this chapter.

Finding Absolute Extrema – In this section we discuss how to find the absolute (or global) minimum and maximum values of a function. In other words, we will be finding the largest and smallest values that a function will have.

The Shape of a Graph, Part I – In this section we will discuss what the first derivative of a function can tell us about the graph of a function. The first derivative will allow us to identify the relative (or local) minimum and maximum values of a function and where a function will be increasing and decreasing. We will also give the First Derivative test which will allow us to classify critical points as relative minimums, relative maximums or neither a minimum or a maximum.

The Shape of a Graph, Part II – In this section we will discuss what the second derivative of a function can tell us about the graph of a function. The second derivative will allow us to determine where the graph of a function is concave up and concave down. The second derivative will also allow us to identify any inflection points (i.e. where concavity changes) that a function may have. We will also give the Second Derivative Test that will give an alternative method for identifying some critical points (but not all) as relative minimums or relative maximums.

The Mean Value Theorem – In this section we will give Rolle's Theorem and the Mean Value Theorem. With the Mean Value Theorem we will prove a couple of very nice facts, one of which will be very useful in the next chapter. Midterm study guidemr. regan's educational website login.

Optimization Problems – In this section we will be determining the absolute minimum and/or maximum of a function that depends on two variables given some constraint, or relationship, that the two variables must always satisfy. We will discuss several methods for determining the absolute minimum or maximum of the function. Examples in this section tend to center around geometric objects such as squares, boxes, cylinders, etc.

More Optimization Problems – In this section we will continue working optimization problems. The examples in this section tend to be a little more involved and will often involve situations that will be more easily described with a sketch as opposed to the 'simple' geometric objects we looked at in the previous section.

L’Hospital’s Rule and Indeterminate Forms – In this section we will revisit indeterminate forms and limits and take a look at L’Hospital’s Rule. L’Hospital’s Rule will allow us to evaluate some limits we were not able to previously.

Linear Approximations – In this section we discuss using the derivative to compute a linear approximation to a function. We can use the linear approximation to a function to approximate values of the function at certain points. While it might not seem like a useful thing to do with when we have the function there really are reasons that one might want to do this. We give two ways this can be useful in the examples.

5 Applications Of The Derivative Part 2ap Calculus Answers

Differentials – In this section we will compute the differential for a function. We will give an application of differentials in this section. However, one of the more important uses of differentials will come in the next chapter and unfortunately we will not be able to discuss it until then.

Newton’s Method – In this section we will discuss Newton's Method. Newton's Method is an application of derivatives will allow us to approximate solutions to an equation. There are many equations that cannot be solved directly and with this method we can get approximations to the solutions to many of those equations.

Business Applications – In this section we will give a cursory discussion of some basic applications of derivatives to the business field. We will revisit finding the maximum and/or minimum function value and we will define the marginal cost function, the average cost, the revenue function, the marginal revenue function and the marginal profit function. Note that this section is only intended to introduce these concepts and not teach you everything about them.

1998 test prepa calculus transcendentals. 1998 AP Calculus AB Scoring Guidelines 1. Let Rbe the region bounded by the xaxis, the graph of y= p x, and the line x= 4. (a) Find the area of the region R. (b) Find the value of hsuch that the vertical line x= hdivides the region Rinto two regions of equal area. (c) Find the volume of the solid generated when Ris revolved about the xaxis. 1998 AP Calculus AB: Section I, Part B x 2 5 7 8 f x 10 30 40 20 85. The function f is continuous on the closed interval 2,8 and has values that are given in the. This 1998 AP® Calculus BC Free-Response Questions AP Test Prep is suitable for 10th - 12th Grade. Provide a test run. Pupils use the questions to practice taking the free-response section of the AP® Calculus BC exam. AP Calculus AB Multiple Choice 1998 Question 86 - 92 86. The base of a solid is a region in the first quadrant bounded by the x-axis, the y-axis, and the line x + 2y = 8, as shown in the figure above. Created Date: 4/21/2006 8:30:01 AM.

5 Applications Of The Derivative Part 2ap Calculus Pdf